ОБХОД ПРЕПЯТСТВИЙ.
ОГРОМНАЯ
ПРОСЬБА: Если кто-то захочет захочет разместить эту статью на
своем сайте, укажите, пожалуйста, в конце ссылку на сайт автора статьи:
http://www.gaze.narod.ru
заранее спасибо.
Отталкиваться в будем от того, что сейчас актуальны алгоритмы, работающие с
большими картами, и сложными препятствиями.
Разумеется, одного алгоритма для нормального
реалистичного передвижения недостаточно. Есть смысл всегда использовать систему
нескольких алгоритмов: для подвижных препятствий нужен быстрый алгоритм, как
правило, позволяющий обойти простые и средние по сложности препятствия. Для
построения маршрута движения по местности необходим алгоритм, требующий
существенных вычислений.
Начать стоит с простых алгоритмов.
Итак,
ПРОСТЫЕ
АЛГОРИТМЫ
Имеется
в виду, что задача таких алгоритмов сводится к определению направления, в
котором нужно сделать один или несколько шагов для продвижения к цели.
Алгоритм правой руки, его недостатки и его
модернизации.
Алгоритм таков. Объекту необходимо выйти из лабиринта. В
соответствии с алгоритмом он поступает следующим образом:
1.
Касается правой
рукой стенки и…
2.
… идет на ощупь
вдоль нее, пока не выйдет.
Недостатки очевидны – не из всякого лабиринта можно выйти
на ощупь, ведь стены могут быть замкнутыми, и объект, фактически прилипший к
стене, будет ходить по кругу.
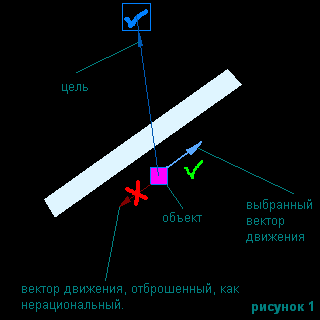
Первая модернизация (рисунок 1), существует довольно-таки давно еще со
времен варкрафта. Вместо движения на ощупь сравнивается расстояние до цели после того как объект продвинется на один шаг вдоль
стены влево и вдоль стены вправо или в
сторону цели, если это возможно. Нужно выбрать тог шаг, который максимально
приблизит объекта к цели. Таким образом, движение уже осуществляется не на ощупь,
а путем анализа близлежащей окрестности.
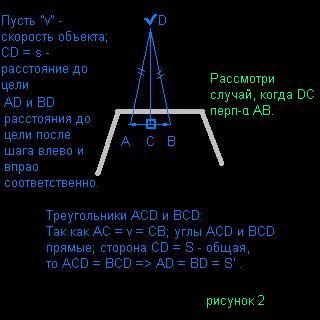
Но бывают такие случаи, когда векторы возможных перемещений оказываются равноправными*, и
тогда движение будет остановлено (рисунок 2).
*имеется в виду что при перемещении в
направлении одного из двух равноправных векторов, объект приблизится к цели
настолько же насколько и при перемещении в направлении другого.
При такой оптимизации алгоритм работает
очень быстро, а препятствия, которые он
позволяет обойти, ОЧЕНЬ простые. Наличие второго однокоренного слова в
предыдущем предложении нежелательно.
Вторая модернизация.
Задача
такова:
1.
нужно двигаться не на ощупь;
2.
поставить такие
условия, при которых не будет ни одной пары равноправных шагов.
Сам алгоритм же примет такую форму:
1.
Если возможно - двигаться к цели.
2.
Если нет, то с
учетом предыдущего направления, выбрать возможное направление движения, при котором объект сможет максимально приблизиться к цели.
На 2-м
пункте остановлюсь поподробнее. Не стоит его понимать буквально. Вот как
расшифровывается не совсем понятное выделенное выражение:
Пусть
объект стоит в точке А, а цель расположена в точке В и
найдена пара векторов перемещения, при которых объект максимально приблизится к
цели двигаясь вправо и двигаясь влево - АС
и АС1 соответственно (рисунок 3).
Следует подобрать
такую систему координат, в которой осью ОХ будет являться вектор АВ, а вектор
предыдущего хода будет лежать в I-й или II-й четвертях или
на оси ОХ. Случай, когда вектор предыдущего перемещения лежит на оси ОХ, назовем
критическим. В критическом случае ось
ОУ следует отложить по
правую сторону (в соответствии с
системой СИ) относительно вектора АВ.
Из АС
и АС1 надо выбрать такой вектор, который с осью ОХ
будет образовывать меньший угол. Если углы одинаковы, выбрать правый вектор.
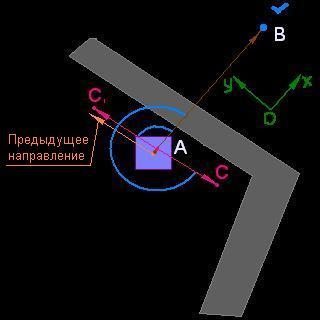
рисунок 3
3.
Переместиться в
выбранном направлении.
4.
Повторять пункты 1-2
до тех пор пока цель не будет достигнута.
При такой модернизации отсутствуют равноправные векторы.
А для выбора направления движения нужно по-прежнему проанализировать только
близлежащую окрестность. Алгоритм работает быстро и позволяет за относительно
небольшое время обойти препятствия средней сложности, например, многоугольник
(необязательно выпуклый).
Алгоритм сканирования.
Алгоритм используется в играх редко,
однако было время, когда он использовался в нашей игре.
Расскажу о нем вкратце. Для простоты
объект примем за квадрат.
0.
Пусть объект стоит в т.А а его цель в точке В. Нужно выбрать систему координат
осью ОХ которой будет являться луч АВ а осью ОУ – луч AD, причем луч AD перпендикулярен лучу АВ и лежит в правой полуплоскости
относительно него.
Из точки А осуществляется
круговое сканирование ( прибираются углы от 0 и до 2Пи
под которыми относительно объекта из точки А откладывается отрезок некоторой
длины и проверяется – не пересекается ли он с препятствием )
Пусть а – текущий угол, под
которым местность анализируется на наличие препятствий, тогда
Ra - расстояние до обнаруженного препятствия (если же препятствие
не обнаружено - Ra стремится к
бесконечности).
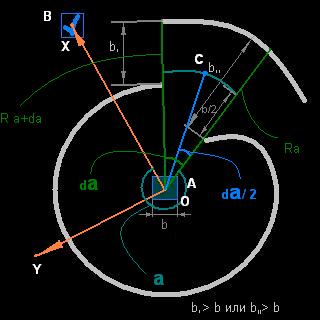
рисунок 4
1.
Нужно найти ближайший
участок а+dа к
оси ОХ, при котором все R ф k (а; dа) *
больше хотябы одного из Ra или R a+da на величину «b»
Где
«b» - ширина
объекта,
da - угол, при
котором объект может пройти между обнаруженными препятствиями на расстояниях Ra и R a+da.
dа
определяется по формуле: dа
>= arcsin(b/min(Ra,R a+da))
* «k» здесь
использовался как знак принадлежности одного множетсва
к другому.
Пусть центр участка – это точка С,
которая удалена от объекта на расстояние
Rc
= min (Ra,R a+da)+(b/2);
и находится под углом a + (da/2) относительно объекта.
2.
После обнаружения вышеописанного участка
объект отправляется в его центр.
3.
Пункты 1 и 2 повторяются до тех пор,
пока объект не достигнет цели.
СЛОЖНЫЕ
АЛГОРИТМЫ
Модернизация
волнового алгоритма обхода препятствий
Принцип действия волнового алгоритма.
Нам даны пункты выхода (А) и конечный пункт
(В).
- Вначале пространство разбивают на секции, как правило они равны ячейкам карты.
- Из пункта В (можно было бы
и из пункта А – разницы нет) начинаем «разливать воду»:
1.1.
Помечаем пункт В как залитый.
1.2.
Перебираем все уже
залитые секции (вначале это только пункт В) и заливаем все соседние секции, не
являющиеся препятствиями.
1.3.
Повторяем пункт 1.2.
до тех пор, пока есть «незалитые» свободные секции.
1.3.1. Если попадается секция, содержащая «А», то из пункта «А»
есть путь к пункту «В».
Самая первая модернизация, которая подробно
описывается в учебниках высшей математики (теория графов) – это перебирать не
все залитые секции, а все только что залитые – грубо говоря (с точки зрения физики), секции «волнового фронта». Все
залитые из этих секций секции образуют новый
волновой фронт. Вот как это можно
реализовать:
- Организуем 2 списка: старый и новый волновой фронт(списки секций).
1.1. В первый список добавляем секцию В,
заранее пометив ее как залитую.
- Организуем «колеблющийся цикл» между двумя этими
списками. Тоесть «каретка» цикла будет номером списка (номер 1-го списка –
0, номер второго - 1). И изменяться она будет при каждой итерации так:
t = |t-1| .Где «t» - значение каретки. Каждый из списков по очереди
является то старым, то новым волновым фронтом.
Цикл будет
выполняться до тех пор, пока текущий список не окажется пустым. Тоесть – волновой фронт
когда-нибудь дойдет до «стенок», границ предоставленного пространства. И как
только все его точки будут «упираться» стенки волна прекратит свое движение и
при следующей итерации нового волнового фронта не образуется.
- Перебираем все секции списка текущего цикла.
3.1.
Находим всех
соседние секции для этой секции.
3.1.1. Если текущая соседняя секция не залита – заливаем
ее, указываем, откуда она была залита, и добавляем в «противоположный список»
(из совокупности добавленных секций в противоположный список будет состоять
волновой фронт на следующем шаге).
3.1.2 Если же текущая соседняя
секция уже залита, значит она либо была залита в предыдущей итерации – либо в
этой, если в этой, то ее уже добавили в противоположный список (новый волновой
фронт) – в любом случае ее можно отбросить.
3.2. Если текущая секция содержит пункт
А (вода льется из пункта В), то результат заливки положительный – из
пункта А можно дойти до пункта В.
Можно объяснить неизбежность выхода из
цикла на другом языке: когда все возможные секции будут залиты, соседних
незалитых секций, которые можно залить, не найдется (что логично), поэтому в
«противоположный список» не будет ничего добавлено – он окажется пустым,
условие выполнения цикла – ложным.
Недостатки традиционного подхода к разбиению на секции.
Под
традиционным подходом подразумевается что ячейки (элементарные
составляющие карты) являются секциями. Тоесть для того
что бы найти путь нужно в среднем перебирать половину от всех ячеек карты
(остальная половина занята объектами). Если карты достаточно большие, например
200*200, то для поиска пути понадобится существенное количество времени.
Рассчитаем его для нашего примера.
Допустим,
что для того чтобы «обработать» полностью одну ячейку нужно 10 байтовых операций,
или 80 битовых. Всего ячеек N = 200*200 = 40 000. Значит для того, что бы полностью залить карту
понадобится около (40 000/2)*80 = 1600000 битовых операций, Тоесть за одну
секунду пи тактовой частоте 500 МГц можно совершить 312 заливок. Если учесть что сократить число битовых операции до 80 возможно только на
ассемблере. То если писать на языке высокого уровня, если вы достигнете хотя бы
100 заливок в секунду, это явление уже можно считать феноменальным. Другими словами этого недостаточно для работы
с большим числом управляемых единиц (У.е.).
Неравные секции.
Придуманный нами метод разбиения на
секции, в данный момент проходит регистрацию в ОФАП.
Тоесть нам нужно добиться
разбиения на минимальное число секций. Ведь накарте
существуют большие незанятые участки, в которые можно помещать квадраты, со
стороной в несколько (иногда в несколько десятков)
ячеек. Это можно сделать следующим образом.
1.
Изначально мы представляем карту в виде одной секции.
2.
Каждую секцию обязательно надо проверить на содержание объектов.
Секцию,
которая содержит объекты, будем называть занятой.
3.
Производим заливку незанятых секций, если волна
не дошла до требуемой точки, Тоесть до
секции содержащей требуемую точку, то заливку будем считать неудачной.
4.
Если заливка неудачна, то разбиваем все занятые секции еще на определенное
число секций по определенным законам (законы
определяются в соответствии с целями и заливки, обычно если заливка
осуществляется в плоском пространстве, то занятые секции делятся на 4 равных
секции).
5.
Заливать (а точнее повторять пункты 2-4) надо до тех пор, пока заливка не будет
удачной либо пока разбивать занятые секции на более маленькие станет
невозможным.
В
связи с тем, что в каждой секции указано место, откуда была залита секция, можно выстроить по
цепочке путь от пункта А к пункту В.
Ниже
приведена примерная картина после разбиения местности на свободные и занятые
секции.
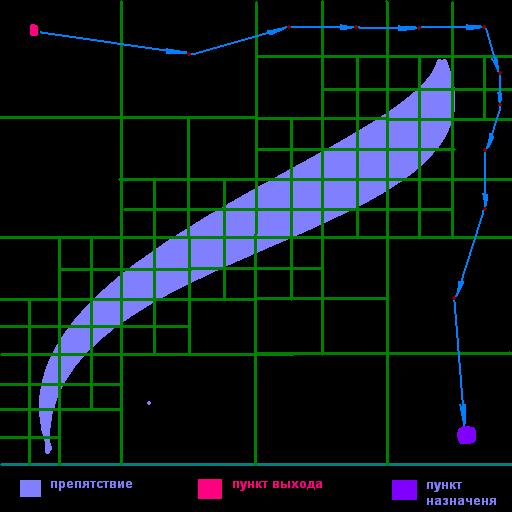
зеленым
кунтуром обозначены образовавшиеся секции.
Такой
подход существенно сокращает время работы заливки.
Если рассмотреть вариант, когда карта не загромождена
мелкими непроходимыми участками, и площадь всех непроходимых участков равна
площади проходимых (что встречается крайне
редко), то обычно все секции в 9 раз больше
ячеек по площади и половина из незанятых секции превышает в 16-64 раза по
площади ячейки карты. Тоесть общее
число незанятых и крайних занятых (секции которых коснется волна)в таком случае будет (S/4)/9+(S/4)/16,
где S общее число ячеек на карте. В нашем случае в
соответствии с этой формулой число ячеек будет
N
= 1736. Тоесть в 11 раз меньше чем при «традиционном разбиении».
Размеры
секций зависят только того, как сильно рассеяны непроходимые участки по карте и
от их общей площади. Такой подход позволяет существенно сэкономить ресурсы
системы и на практике, в среднем, он может ускорить процесс заливки в сотни и
тысячи раз.
Дятковский Степан.
StpMail@avtograd.ru